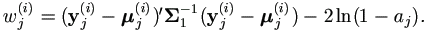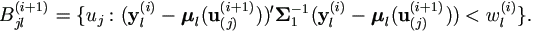Chapter 6 Sampling in MCEM Algorithm
In this Chapter, we detail the sampling scheme needed in the MCEM algorithm implementations outlined in Theorem 4.2 and Theorem 4.5. The augmented Gibbs sampler developed in Theorem 6.3 is very efficient and particularly suitable for sampling from truncated distributions and for EM style algorithms.
Let us first briefly review some widely used sampling methods and algorithms, which are relevant to our implementation schemes.
Inverse Cumulative Distribution Method
This is a well known method for generating a (univariate) variable X with cumulative distribution function F. It is particularly attractive in designing efficient Monte Carlo methods (Johnson, 1987; Olkin et al., 1980). The method is stated simply as
Lemma 6.1. A variate X under distribution function F can be generated as follows.
| (1). | Generate a variate U from uniform distribution U(0,1). |
| (2). | Let X = supx[F(x) ≤ U ]. If F is strictly increasing, let X = F-1(U ). |
Method of Composition
The method of composition (Tanner, 1996) is essential for generating multivariate random variables from univariate sampling.
Lemma 6.2. Suppose ƒ(y|x) and g(x) are density functions where x and y may be vectors. Repeat the following two steps m times.
(1). Draw x* ~ g(x).
(2). Draw y*~ ƒ(y|x*).
The pairs (x1, y1), ..., (xm, ym) are an i.i.d. sample from the
joint density h(x, y)=ƒ(y|x)g(x), while y1, ..., ym are an i.i.d. sample from the marginal
Theoretically, we can generate random variables with any dimension with this lemma. The method is a key technique underlying the data augmentation algorithms.
The Gibbs sampler is a powerful Markov Chain Monte Carlo (MCMC) data augmentation technique (Geman & Geman, 1984; Gelfand & Smith, 1990). It has been widely utilized in the image-processing and other large scale models such as neural networks and expert systems. The general problem is to draw (dependent) samples from a very complex multivariate density. Suppose that y is a k×1 random vector with density ƒ(y), also that the following conditional distributions are known,
Lemma 6.3. (Gibbs Sampler)
Given an arbitrary starting point in the support of ƒ(y) as
For j = 1, ..., k, draw yj(i+1) from
The vectors y(0), y(1), y(2), ... are a realization of a Markov chain with transition probability from
y(i) to y(i+1) as 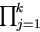 ƒj(i+1).
ƒj(i+1).

These results suggest that if the chain is run to equilibrium, one can use the simulated data as a basis for summarizing ƒ(y), and the average of a function of interest over values from a chain yields a consistent estimator of its expectation.
In practice, we need to discard some initial iterations as ``burn-in" steps so that the sampling is not far from the converged distribution. If an iid sample is desired, multiple independent chains with different starting points or suitable spacings between realizations could be employed. Also, determining run length and assessing convergence are important practical issues (Brooks & Gelman, 1998; Tanner, 1996). A good explanation of Gibbs sampler can be found in Casella and George (1992).
Two other widely used sampling algorithms are data-augmentation (Tanner & Wong, 1987) and sampling-importance-resampling (Rubin, 1987). Gelfand and Smith (1990) compared them with the Gibbs sampler to the calculation of marginal densities and obtained some favorable findings to the Gibbs sampler and the data-augmentation algorithm. As they argued, the two iterative methods are closely related, and the latter could slightly speed up the Gibbs sampler if more reduced conditional densities are available.
6.2 Sampling from Conditional Densities k1 and k2
In this section, we discuss the sampling scheme from general distributions. From next section on, we deal with multivariate normal distribution in particular, wherein a rather attractive Gibbs sampler is developed, which could be generalized to many general distributions.
Sampling from Conditional Distribution k1
When some components of y is not completely known, we need
to generate random samples of y from the conditional
distribution k1(y|u,  ) given in equation (4.6) as
) given in equation (4.6) as
 .
.
This is a density function over  *, the observed range of incomplete components of y. It is easy to rewrite it in terms of conditional distribution as
*, the observed range of incomplete components of y. It is easy to rewrite it in terms of conditional distribution as
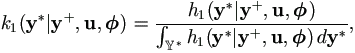 | (6.1) |
which is a truncated density of h1(y*|y+,u, ). Sampling from such distribution, especially the truncated multivariate
normal distribution, has been very well studied in the literature and
usually can be handled by the Gibbs sampler or other Markov Chain
Monte Carlo (MCMC) methods such as the Metropolis-Hastings algorithm
(Metropolis et al., 1953; Hastings, 1970). As an added advantage of these
MCMC methods, the integral calculation in the denominator of
(6.1) can usually be avoided.
). Sampling from such distribution, especially the truncated multivariate
normal distribution, has been very well studied in the literature and
usually can be handled by the Gibbs sampler or other Markov Chain
Monte Carlo (MCMC) methods such as the Metropolis-Hastings algorithm
(Metropolis et al., 1953; Hastings, 1970). As an added advantage of these
MCMC methods, the integral calculation in the denominator of
(6.1) can usually be avoided.
Sampling from Conditional Distribution k2
The key step is to generate random samples of u from the
conditional distribution k2(u| ,
, ) given in
equation (4.7) as
) given in
equation (4.7) as
 | (6.2) |
For simplicity, assume u is a scalar. However, it is not
difficult to extend it to a vector. Denote the cumulative distribution
function of k2(u| ,
, ) by
) by

which is continuous in our context.
By the inverse cumulative distribution method in Lemma 6.1, we have
Lemma 6.4.
To generate a sample of size m from
k2(u| ,
, ), proceed as follows.
), proceed as follows.
(1). Draw a sample a(1), a(2), ..., a(m) from uniform distribution U(0, 1).
(2). Solve the equation K2(u) = a(i) for u to get u(i).
Then sample u(1), u(2), ..., u(m) is such a random sample
from k2(u| ,
, ).
).
The equations in step (2) can be solved by simple numerical algorithms such as the bisection method or the Newton's method. Now the problem becomes how to calculate K2(u) when u is known. Denote function
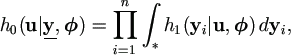 | (6.3) |

Let I(.) be the indicator function. For given v,
 | (6.4) |
Now we need to calculate the two expectations above with respect to
h2(u| ).
).
Lemma 6.5. For any given v, we can proceed as follows with a sample of size m.
(1). Draw a sample u(1), u(2), ..., u(m) from  ).
).
(2). Calculate expectations as
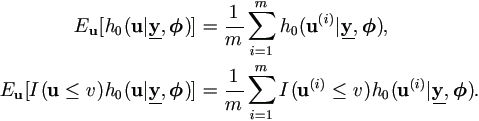
Now we need to calculate
 ,
, )
) h1(yi|u,
h1(yi|u, )dyi
)dyi
Case (a), if all components of yi are complete, it is simply
 h1(yi|u,
h1(yi|u, )dyi
= h1(yi|u,
)dyi
= h1(yi|u, ).
).
Case (c), if all components of yi are incomplete, i.e.
yi 
 i, we have
i, we have

Now the calculation can be done by the following simulation.
(1). Draw a sample yi(1), yi(2), ..., yi(m) from  i under
i under
 ).
).
(2). Calculate  h1(yi|u,
h1(yi|u, )dyi
)dyi .
.
Case (b), if some components of yi are incomplete, say
yi = (yi+, yi*)  {yi+} ×
{yi+} ×  i*,
i*,
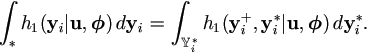
That is, plug in completely observed components yi+ into
the integrand and then integrating over  i* for incomplete components.
i* for incomplete components.
Since in general
 )
) )
)
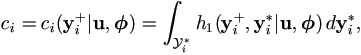
where
 i* is the sampling space for yi*, and ci could be calculated by Monte Carlo method if no closed form solution is available. This results the conditional distribution
density function for yi* given
i* is the sampling space for yi*, and ci could be calculated by Monte Carlo method if no closed form solution is available. This results the conditional distribution
density function for yi* given
 )
) )
) )/ci.
)/ci.

Lemma 6.6.
The calculation of
 ,
, )
)
(1). Draw a sample
yi*(1), yi*(2), ..., yi*(m) from  i* under
i* under
 ).
).
(2). Calculate
 h1(yi|u,
h1(yi|u,  ) dyi
) dyi .
.
Note that case (c) is a special case where ci = 1, and case (a) is
also a special case with  )
)
Theorem 6.1.
A sample of u from the conditional distribution
k2(u| ,
,  ) can be drawn as follows.
) can be drawn as follows.
(1) Draw a sample a(1), a(2), ..., a(m) from uniform distribution U(0, 1).
(2) Draw a sample u0(1), u0(2), ..., u0(m) from
h2(u|  ).
).(3) Calculate
h0(u0(j)| for j = 1, 2, ..., m as follows. ,
, )
)(3.1) For i = 1, ..., n and j = 1, ..., m, calculate
 h1(yi|u0(j),
h1(yi|u0(j),  ) dyi
) dyi(a) if yi is completely known, let
 h1(yi|u0(j),
h1(yi|u0(j),  ) dyi
) dyih1(yi|u0(j), . )
)(b) if some components of yi are incomplete, draw a sample of yi* from
 i* as
i* as
yi*(j,1), yi*(j,2), ..., yi*(j,m) underh1(yi*|yi+, u0(j), let ),
),
(c) if all components of yi are incomplete, draw a sample of yi from
 i as
i as
yi(j,1), yi(j,2), ..., yi(j,m) underh1(yi|u0(j), let ),
),
(3.2) Calculate
h0(u0(j)| = ,
, )
)
 h1(yi|u0(j),
h1(yi|u0(j),  ) dyi
) dyi(4) Solve the equation
 for u to get u(i) for i = 1, 2, ..., m, where
for u to get u(i) for i = 1, 2, ..., m, where

 ,
, ).
).
6.3 Mixed Models with Normal Distribution
Under multivariate normal distribution, we can design a very attractive Gibbs sampler employing the idea of latent variables (Damien & Walker, 1996). This method is remarkably suitable for truncated densities and EM style algorithms. It is very easy to implement and bypasses the need for rejection sampling and algorithms such as the Metropolis-Hastings and sampling-resampling. With the introduction of one or more latent variables, most conditional distributions can be sampled via uniform variates. It is applicable in a very broad range of distributions.
6.3.1 Normal Model
For the Mixed model given in equation (4.2),
For multivariate normal distribution
 ) ~
Nk(μi, Σ1),
) ~
Nk(μi, Σ1), )
) )
) )
) , then
, then
 | (6.5) |
then the marginal distribution of
 )
) )
) (yi+- μ+)
(yi+- μ+) Σ+*.
Σ+*.
 | (6.6) |
where k+ and k* are the number of complete and incomplete components of yi, respectively.
6.3.2 Sampling from  )
)
Now discuss the sampling from  ),
),
 i*,
i*,
 )
)
 h1(yi*|yi+, u,
h1(yi*|yi+, u,  )
I(yi*
)
I(yi*
 i*).
i*).
We will construct a general Gibbs sampler from truncated multivariate
normal distributions, with sampling from
 )
)
Given matrix A = (aij), let vector a(j) be the jth column of A without the jth element ajj, and matrix Ajj be the sub-matrix of A without the jth row and column.
Lemma 6.7 Suppose x=(x1, ..., xk)' and matrix A = (aij)k×k. Given xi (i ≠ j) and y, if ajj > 0, the solution of xj from the quadratic inequality x'Ax < y is given as xj(l) ≤ xj ≤ xj(r), where
 | (6.7) |
and x(j) is the vector x without the jth element xj.
If A is diagonal as A={d aii}, the roots in equation (6.7) become
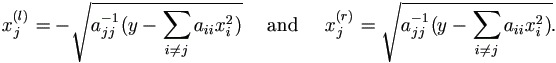 | (6.8) |
Now we state the following augmented Gibbs sampler for truncated multivariate normal distributions, which is implied in Cumbus et al. (1996).
Theorem 6.2
Suppose  A, say
A, say
(1). Given an arbitrary starting point
x(0)=(x1(0), ..., xk(0))'  A. Set counter i = 0.
A. Set counter i = 0.
(2). Draw a ~ U(0, 1) and let
y(i) = x'(i)  x(i) - 2ln(1 - a).
x(i) - 2ln(1 - a).
(3). For each j, in the order from 1 to k draw xj(i+1) from uniform distribution over the set
 , where
, where  .
At the end of this step, we have
.
At the end of this step, we have
When i is large enough (after initial burn-in period),
x(i+1) is approximately from
Proof. With a latent variate y, easy to verify that the joint density

has its marginal density for x as
 A. In order to show that the theorem is a Gibbs
sampling of (x, y) from the joint density ƒ(x, y),
we only need to show that step (2) is in fact sampling y(i) from
ƒy|x(y|x(i)), and step (3) is sampling xj(i+1) from
A. In order to show that the theorem is a Gibbs
sampling of (x, y) from the joint density ƒ(x, y),
we only need to show that step (2) is in fact sampling y(i) from
ƒy|x(y|x(i)), and step (3) is sampling xj(i+1) from  .
.
Based on the joint distribution ƒ(x, y), given x,
variate y has truncated exponential distribution
 , which can be sampled by the inverse cumulative distribution method. It is done in step (2).
, which can be sampled by the inverse cumulative distribution method. It is done in step (2).
On the other hand, given y, vector x has multivariate
uniform distribution over the region  x<y}∩A.
x<y}∩A.
 I(x'
I(x' x<y,
xj
x<y,
xj  Aj),
Aj),
over the set
 x<y}∩ Aj.
x<y}∩ Aj.
Note that (ai, bi) could have ai=-∞ or bi=+∞. In fact, the bounding set A could be far more complex than intervals.
Since
 )
)
 h1(yi*|yi+,u,
h1(yi*|yi+,u, )
I(yi*
)
I(yi*
 i*),
i*), )
) (yi+- μ+)
(yi+- μ+) Σ+*.
Σ+*. )
)
Corollary 6.1
Drawing a variate yi* ~
 )
)
(1). Calculate μ0 =
μ* +  (yi+-μ+)
(yi+-μ+) Σ+*.
Σ+*.
(2). Draw y0 ~
Nk*(0, Σ0)
over the region A = {y0: y0 + μ0 
 i*} as above.
i*} as above.
(3). Let yi* = y0 + μ0, then yi* is a drawing from  )
) i*.
i*.
6.3.3 Sampling from  ,
,  )
) |
| ,
,  )
)
Now we employ similar idea of latent variates to implement a Gibbs
sampler for drawing u from the conditional distribution
 ,
,  )
)
 | (6.9) |
In fact, sample  from the conditional distribution
from the conditional distribution
 |
| ,
,  )
)

Let latent variables w1, ..., wn, v together with y1*, ..., yn*, u have joint density

Note that yi =  i*, and
μi is a function of u =
i*, and
μi is a function of u =
It is easy to verify that based on this joint distribution, the marginal density function for u is
 ,
,  )
) ).
). ,
,  )
) )
) |
| ,
,  ).
).
The following conditional densities are easy to obtain and essential for Gibbs sampling. Given all other variables, each yij and uj has uniform distribution, while wi and v have truncated exponential distributions. All of these distributions are very easy to sample from.
If yij is incomplete, given all other incomplete y's, as well as u, v, w's,
where Aij = {yij: (yi - μi)' (yi - μi) < wi}, which can be obtained by (6.7). This is a univariate
uniform distribution over set Aij ∩ {yij: yi*
(yi - μi) < wi}, which can be obtained by (6.7). This is a univariate
uniform distribution over set Aij ∩ {yij: yi*

 i*}.
i*}.
For each component uj of u,

It is a uniform distribution over the set

Given y* =( y1*, ..., yn*) and u, wi and v have truncated exponential distributions

 (yi - μi)
(yi - μi) u,
u, |
| ,
,  ),
), ,
,  ),
), )
)
Theorem 6.3
Assume  is known. An augmented Gibbs sampler for
is known. An augmented Gibbs sampler for
 |
| ,
,  )
) ,
,  )
)
| (1). | Select staring points for u and yj for j = 1, ..., n, and set counter i = 0.
|
||||
| (2). | Draw a ~ U (0, 1). Let  |
||||
| (3). | For j = 1, ..., n, draw aj ~ U (0, 1). Let
|
||||
| (4). | In the order of j from 1 to q draw
 and and
|
||||
| (5). | For j = 1, ..., n, get yj(i+1) =( yj1(i+1), yj2(i+1), ..., yjk(i+1))' as below.
In the order of l from 1 to k,
if yjl is completely known, set  ,
where ,
where  and and
|
When i is large enough (after initial burn-in period),
 ,
,
 ),
),
 1) and
1) and
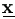 (i+1)
(i+1)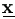 |
| ,
,
 ).
Repeat steps (2-5) with i+1 to sample more points.
).
Repeat steps (2-5) with i+1 to sample more points.
Note that the bounding sets in steps (4) and (5) can be obtained by equation(6.7).
This Gibbs sampler is very efficient and will be used in our subsequent simulations and data analysis. More importantly, the use of latent variables in constructing the augmented sampler is an ideal match for sampling incomplete data in EM style algorithm. Its potential could be enormous in sampling schemes for very complicated distributions and in other areas as well.