Gaussian elimination

Gaussian elimination is a method for solving linear systems. The basic idea is to transform a square system into an upper triangular system of equations which is easier to solve. This is accomplished using three elementary row operations which change the form of a linear system without changing the solution . In order of potential usefulness they are

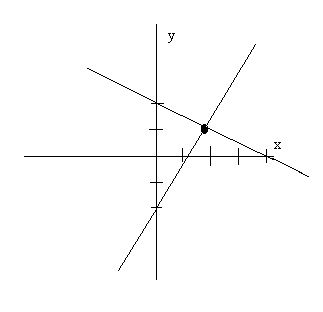
Permutation does not change the solution of a linear system since it does not matter what order the equations are written in. Scaling does not change the solution of a linear system since multiplying an equation by a nonzero number does not change the solution. To see why elimination preserves the solution consider the linear system below with solution (2,1) 

æ  x + 2y = 4 ö
è 3x - 2y = 4 ø
with graph
Lines
Subtracting 3 times row 1 from row 2 to yields 

æ  x + 2y =  4  ö
è     -8y = -8  ø
with graph
More lines
Comparing the graphs we note that the lines have been rotated without changing the point of intersection.

Example:     Solve 
æ 2x +  y +  z = 180 ö
ç  x + 3y + 2z = 300 ÷
è 2x +  y + 2z = 240 ø

é  2  1  1 | 180  ù
ê  1  3  2 | 300  ú
ë  2  1  2 | 240  û

 R1 <  > R2
The pivot element is the first nonzero entry in the row which does the elimination. The pivots are usually found along the diagonal. When doing the arithmetic without a computer we can often avoid fractions by making sure the pivot element is 1. In this problem we can accomplish this by exchanging rows 1 and 2. This is an optional step. 

é  1  3  2 | 300  ù
ê  2  1  1 | 180  ú
ë  2  1  2 | 240  û

 R2   > R2 - 2 R1 
 R3   > R3 - 2 R1
The goal of the gaussian elimination process is to zero out the entries below the diagonal using the elimination step. The elimination step involves replacing a row with itself minus a multiple of another row. The multiple is computed using 

               entry to eliminate 
 multiplier =                    .
                    pivot
We now proceed to zero out the entries below the first diagonal entry. The required multipliers are 2/1 = 2 and 2/1 = 2. The calculations leading to a new row 2 are 2-2(1) = 0, 1-2(3) = -5, 1-2(2) = -3, 180-2(300) = -420. The calculations leading to a new row 3 are 2-2(1) = 0, 1-2(3) = -5, 2-2(2) = -2, 240-2(300) = -360. Notice that each time you zero out an element you must change an entire row. 
é  1  3  2 | 300  ù
ê  0 -5 -3 |-420  ú
ë  0 -5 -2 |-360  û

 R3   > R3 - R2
We now zero out the entry below the second diagonal element. The required multiplier is -5/-5 = 1 and the calculations leading to a new row 3 are 0-1(0) = 0, -5 -1(-5) = 0, -2-1(-3) = 1, -360-1(-420) = 60. 
é  1  3  2 | 300  ù      æ x +   3y + 2z = 180  ö
ê  0 -5 -3 |-420  ú  OR  ç      -5y - 3z = -420 ÷
ë  0  0  1 |  60  û      è             z = 60   ø
The system of linear equations above is equivalent to the original system but it is much easier to solve. The third equation has only the variable z and it is easy to solve for z = 60. The second has variables y and z but z already determined and so we can easily solve for y. 5y - 3(60) = -420, -5y = -240, OR y = 48. The first equation has variables x,y and z but y and z have already determined and we can easily solve for x. x + 3(48) + 2(60) = 300, x + 144 +120 = 300, x = 36 This process is called back substitution. Hence, the solution is 
æ x = 36 ö
ç y = 48 ÷
è z = 60 ø

Exercise

(1)     Solve 
æ 2x +  y +  z = 180  ö
ç  x + 3y + 2z = 300  ÷
è 2x +  y + 2z = 240  ø

 x = 2, y = 1, z = 3
 x = 3, y = 4, z = 1
 No solution.
 Infinite number of solutions.

| Table of Contents | | Previous | | Next |