

GENERALISED AFFINE & PROJECTIVE SPACES
Classical affine and projective spaces have a simple relationship: removing part of a projective space leaves an affine subspace of the same dimension as the original projective space. Consider, for example, the 15 point projective 3-space. Removing a 7 point projective plane (the ideal plane) leaves an 8 point affine 3-space. Intuitively, we can picture the 8 corners of a cube as the eight points. These 8 points can be "connected" in various ways. There are 14 projective planes which connect affine points, each plane intersecting the ideal plane in a line. The ideal plane is on exactly 7 ideal lines and each ideal line is on exactly two projective planes that intersect the 8 affine points in two parallel affine planes, each with exactly 4 points. The cube has 6 faces, representing three sets of two parallel affine planes. Of course, this leaves four more sets of two parallel affine planes. Six faces plus eight more planes makes the total of 14 planes which intersect the affine 3-space.
Classical affine spaces can also have points connected by "vectors". The concept of a vector shows an important relationship between algebra and geometry. A projective N-space can be described by points, lines, planes, etc. and their relationships are expressed by postulates. With an additional postulate, some permutations of points have a geometric significance: they may also induce permutations of lines, planes, etc. In the case of a projective plane, when a permutation of points also induces a permutation of lines, it is called a collineation. Certain collineations may fix every point of a projective line. A special collineation called a plane elation fixes every point of an ideal line and every line on some ideal point, called a center, is also fixed as a line. Projective elations give rise to affine vectors which connect affine points. But only certain projective spaces have the property that any two affine points are connected by a unique vector. Such projective spaces are called desarguesian, in honor of the French mathematician, Girard Desargues (1591-1661), who first introduced the principal concepts of projective geometry.
There is a deep relationship between classical affine spaces and classical vector spaces. It appears that desarguesian affine spaces are important for physics because any two points in such a space are connected by a unique vector from a classical vector space. Non-desarguesian affine spaces appear to have an insufficient number of vectors connecting their points. Such spaces are mathematically interesting but lack the vector structure to do physics.
As an illustration of a desarguesian affine plane, consider the relatively simple 13 point projective plane with an affine subplane of 9 distinct points. Each projective point is on exactly four distinct projective lines and each projective line in on exactly four distinct projective points. If we remove one ideal line (of four points), then we have an affine subplane of 9 points. It can be shown that the finite field Z(3) is related both to the 13 point projective plane and the 9 point affine subplane. In fact, the two dimensional vector space Z (3)+Z(3) can be used as a coordinate system for the 9 affine points in such a way that any two affine points are connected by a unique vector.
Finite desarguesian projective planes are of considerable interest. The simplest one has seven points and seven lines. Each point is on exactly three lines and each line is on exactly three points. The vector space connecting any of its affine subplanes is Z(2)+Z (2). In the previous paragraph, we saw that the 13 point projective plane is related to finite field, Z(3). There is a projective plane with 21 points and 21 lines. It has an affine subplane of 16 points. This affine subplane is connected by a classical vector space, but not related to the ring Z(4). To begin with, Z(4 ) is a ring but not a field. Classical finite vector spaces are always related to finite fields. There is a finite field with four elements and it is called a galois field (GF(4)), in honor of the French mathematician Evariste Galois (1811-1832), famous for his contributions to the branch of algebra known as group theory.
Each point of the 21 point projective plane is on exactly 5 projective lines and each line is on exactly 5 points. Removing an ideal line (of five points) leaves an affine subplane of 16 points which are connected by the two dimensional vector space GF(4)+GF(4). The projective planes of 7, 13 and 21 points are well known as are the vector spaces which connect their affine subplanes.
But there is a question which remains about the ring Z(4). Even though this ring is not a field, one would still expect some kind of geometric structure and some kind of vector space structure related to this ring. Although it is not commonly known, this ring gives rise to a generalized projective plane with 28 points and 28 lines. Unlike the other examples shown above, the relationship between the projective plane and the affine subplane is more complicated.
Although Z(4)+Z(4) is not a classical vector space, it does have a generalized vector space structure. In classical terms, Z(4)+Z(4) is a two dimensional unitary module over ring Z(4). If we call the elements of this module "vectors", what does it mean for a set of vectors to be linearly independent? Let a be any element of Z(4) and consider the scalar multiple a(1,0). This can only be the zero vector (0,0) if a = 0. On the other hand, 2(2,0) = (0,0). One is tempted to say vector (1,0) is linearly independent but vector (2,0) is linearly dependent. Generalizing to any set of vectors y(1), y(2), . . . , y(k) we say they are linearly independent if and only if a(1)y(1) + . . . + a (k)y(k) = (0, . . ., 0) implies a(i) = 0 for i = 1, . . . , k. Of the 16 vectors in Z(4)+Z(4), 12 are linearly independent and 4 are linearly dependent. Clearly, the dependent ones are (0,0), (2,0), (0,2) and (2,2).
As a generalized two dimensional vector space Z(4)+Z (4) can be thought of as the sum of two linearly independent cyclic submodules: <(1,0)>+<(0,1)>, <(1,2)>+<(1,1)> etc. This generalized vector space with 16 vectors connects an affine suplane of 16 points. So why is it that the projective plane here has 28 points instead of the smaller 21 points coming from the galois field? This is a fascinating question and requires looking at the generalized vector space Z(4)+Z(4)+Z(4) which has dimension three and is composed of 64 vectors. A relatively simple process leads to a new discovery in projective geometry.
Over the coming months more information can be made available including a postulate system for generalised finite desarguesian projective planes and detailed examples to illustrate the general theory. We have built a physical model for the 28 point plane based on ring Z(4). It is composed of 16 red light emitting diodes (LEDs), arranged in a square and they are surrounded by two hexagons of green and amber LEDs. The red LEDs represent affine points and the green and amber LEDs represent the 12 ideal points. There are four ideal lines, each composed entirely of six ideal points. There are 24 other projective lines, each composed of four affine points and two ideal points.
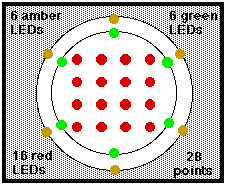
Peter Schmedding designed and built the electronic model of the 28 point plane. When a button representing a line is pressed, six LEDs light up representing the six points on that line. The model is very sophisticated because two distinct 28 point planes can be shown on the one electronic model.
Anyone who is interested in these ideas may contact us by e-mail.
* * *
Copyright ©1997 - 2001 Bob Stephenson PhD and Peter Schmedding, Canberra Australia.