PROFUNDIZANDO EL CONCEPTO FRACTAL (

NÚMEROS COMPLEJOS (1)

La Crisis de la Matemática: Una extensión a los Reales.

Cuando ya se conocía el conjunto numérico de los Reales, una pregunta muy simple vino a provocar una verdadera crisis en los estudiosos de esa época.

La pregunta era: "¿Cuál es la raiz cuadrada de -4?". Por supuesto que el poco tino de algunos señaló: "2". Pero estaban muy equivocados. Recordemos que se define raiz cuadrada ("popularmente") como el número que multiplicado por si mismo 2 veces da como resultado el número bajo raiz. Entonces, la raiz cuadrada de 4 es 2, porque 2 por 2 es 4, pero no podemos decir que sea 2 para raiz cuadrada de -4, porque 2 por 2 siempre será +4 ("positivo"). De igual forma no podemos señalar que sea -2, porque -2 por -2 es +4 (regla de multiplicación y otras más para confirmarlo). Podemos demostrar eso fácilmente.

Si mal no recuerdo, fue Benginni quien propuso por primera vez el concepto de Número Imaginario. Ante la imposibilidad de encontrar una respuesta para las raices pares de números negativos, los matemáticos optaron por una solución: ese número "no existía". Pero afirmar que algo "no existe" por sólo no poder econtrarlo es difícil. Por lo cual, el genial matemático Rene Descartes ("decart") propuso el concepto de Número Complejo en base a un número Real y a un número que era "imaginario" (porque, como no existía físicamente, se imaginaba).

La Unidad Imaginaria: Raiz Cuadrada de -1.

Decir que un número no existía resultó complejo (valga la redundancia). Por tanto, se adoptó la Unidad Imaginaria que correspondia a la unidad del nuevo conjunto que había nacido, el de los Número Imaginarios o Irreales. La raiz cuadrada de -1 representaba esta unidad y podía ser operada de distintas maneras. Gracias a ella se logró resolver el problema de las raices pares de números negativsos, ya que se encontró solución para cualquier raiz de ese tipo.

Por ejemplo, se tenía el siguiente proceso para resolver una raiz simple:

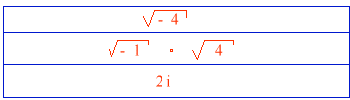
El ejemplo nos muestra la raiz cuadrada de -4. Podemos descomponerla como el producto de raices de igual indice, es decir, raiz cuadrada de -1 y de 4. Pero raiz cuadrada de -1 es la unidad imaginaria (i), por lo que podemos escribir el resultado como i por raiz cuadrada de cuatro. Y la raiz cuadrada de cuatro es 2. Entonces el resultado final es 2i.

De igual forma, existen las potencias de "i". Por ejemplo, si "i" es raiz cuadrada de -1, enconces i al cuadrado es raiz cuadrada de -1 al cuadrado, lo que es -1 y así. Las potencias de "i" entregan sólo 4 valores, que van de 1, i, -1 y -i. Esto suele reducirse a una fórmula de la forma i elevado a 4n para encontrar las soluciones de las raices que sean números pares y otras para las que sean impares como 4n + 1.

Se Introducen los Complejos: el descubrimiento de Descartes.

No podría afirmar que fue realmente Descartes quien "descubrio" los Números Complejos, pero sí se hace referencia histórica a que fue el primero en introducirlos a la matemática.

Cuando se conocían los número Imaginarios (o llamados comunmente el conjunto "I"), se generó otro conjunto más grande aún, ya que era la extensión para los otros dos conocidos, los Reales y los neonatos Irreales. Este conjunto tomó el nombre de "Números Complejos" (abreviados como "C") y su estructura estaba dada por un par ordenado de la forma:

Z = ( A , B )

En este par ordenado, A representaba a un número Real cualquiera y B era un número Imaginario. De esta forma, números como (3, 4i) o (5, i) eran Complejos. Este conjunto poseía propiedades y operaciones. Por ejemplo, podía multiplicarse, tanto como par ordenado o de la forma algebráica A + Bi, donde A y B son reales e "i" es la unidad Imaginaria.

Reales e Imaginarios: Del Plano Cartesiano, al Plano Complejo.

Al introducir el conjunto de los Complejos, se dio además un nuevo paso desde el antiguo plano Cartesiano al plano "Complejo". Este nuevo plano de representación de pares ordenados constaba de un eje x o de absisa donde se colocaban todos los números Reales, y un plano de eje y u ordenadas donde se colocaban todos los imaginarios. Luego, cualquier punto en ese plano tendría una componente (X,Y) que sería un número complejo.

El Conjunto de Mandelbrot: la Iteración de un Complejo.

EI conjunto de Mandelbrot que hemos conocido en estas páginas (o que vamos a conocer, aunque de hecho aparece en el fondo de todas las webs de este sitio) es la iteración de un número complejo simple. Este número, claro está, es de la forma A + Bi. El proceso de iteración aparentemente es simple (bueno, de hecho lo es), ya que consiste en tomar el número y elevarlo al cuadrado y luego sumarle a todo ese resultado el mismo número complejo. Luego repetir el proceso infinitas veces. Obviamente, si lo hacemos por cálculo algebráico, el resultado iría haciéndose cada vez más y más complejo, hasta ya casi no poder operarlo. Por suerte, Mandelbrot contaba con el apoyo de las poderosas computadoras de la IBM cuando descubrió su Conjunto y la representación de este en pantalla arrojó una imagen impresionante, que por su "fragmentación" decidió llamar FRACTAL.

INICIO | CUERPOS FRACTALES | GENIOS CREADORES | PROBLEMAS FRACTALES | IMÁGENES FRACTALES