Cuando una función multimodal de una variable es discreta, la interpolación cúbica no sirve (puesto que la función no es diferenciable en los puntos de discontinuidad), y los métodos de Fibonacci y sección de oro tampoco sirven, puesto que la función, aún siendo discreta, no es unimodal. En estos casos el método de interpolación cuadrada es el apropiado.

Este método fue diseñado por Powell y mejorado más tarde por Zangwill .Se presenta aquí la versión original de Powell, que consiste en tres fases. Fase 1. Dados valores de un punto arbitrario X y una dirección arbitraria s, evalúe

El punto X es el punto de partida de la búsqueda del óptimo local, mientras que s es la dirección de la búsqueda.

Fase 2. Evalúe g(a) para a = 0, 1, 2, 4, 8, 16,...,a, b, c, donde c es el primer valor de a para el cual g(a) se ha incrementado. El valor óptimo de a, a* , se encuentra en el rango a < a* < c. Fase 3. Una vez que se conocen los valores de g(a), g(b), g(c) se ajusta un polinomio cuadrado a f(X) y se calcula el mínimo local del polinomio, ae dado por:

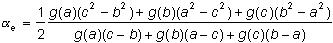
Si g(ae) < g(b) entonces a* = ae .De otra manera, es decir, si g(ae) > g(b), se toma a* = b.